Dissertativa 10 - 2ª Fase - Dia 1 - IME 2026

Novidade! Correção inteligente - simulado seus resultados.

Clique aqui e veja a resolução ITA 1ª Fase 2026

Selecione uma prova

Gabarito

Matemática
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 10

Dissertativa

Seja o tetraedro regular ABCD de aresta a e a esfera inscrita no mesmo. Considerando cada vértice, traça-se um plano distinto da base oposta, paralelo a esta base e tangente à esfera. Um novo tetraedro é então formado a partir do vértice A e dos novos vértices definidos pela interseção do novo plano traçado, paralelo à base BCD, com o tetraedro ABCD. Analogamente faz-se o mesmo processo para os vértices B, C e D. Em seguida, inscreve-se uma esfera em cada novo tetraedro criado. Repete-se o processo de forma indefinida. Calcule em função de a o volume ocupado por todas as esferas interiores ao tetraedro ABCD.

Resolução:

Sabe-se que:

1) A altura h do tetraedro regular de aresta a é dada por:

$h = \frac{a \sqrt{6}}{3}$

2) O raio da esfera inscrita no tetraedro é dado por:

$r = \frac{h}{4} = \frac{a \sqrt{6}}{12}$

E seu volume é dado por:

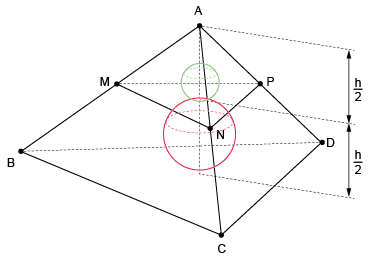
$v_{o} = \frac{4 π}{3} r^{3} = \frac{4 π}{3} {(\frac{a \sqrt{6}}{12})}^{3} = \frac{π \sqrt{6}}{216} a^{3}$

Assim, o plano paralelo à face BCD que tangencia a esfera inscrita distará $2 r = \frac{h}{2}$ de BCD, passando pelos pontos médios M, N e P de $AB, AC e AD$ . O tetraedro AMNP é semelhante a ABCD com razão de semelhança $k = \frac{1}{2}$ . O raio da esfera inscrita em AMNP é, portanto, metade do raio da esfera inscrita em ABCD, sendo seu volume igual a $k^{3} = \frac{1}{8}$ de $v_{0}$ .

De maneira análoga, os planos paralelos às outras faces de ABCD delimitarão esferas com volume de $\frac{1}{8}$ de $v_{0}$ . Dessa forma, nesse primeiro passo, criam-se 4 esferas com volume $\frac{1}{8}$ de $v_{0}$ .

O processo segue de maneira recursiva: cada novo tetraedro dá origem a 4 novos tetraedros e a 4 novas esferas com volume $\frac{1}{8}$ do volume do passo anterior, ou seja, a cada novo termo da soma multiplicam-se as esferas por 4 e o volume de cada esfera por $\frac{1}{8}$ .

A soma dos volumes de todas as esferas será dada por:

$v = v_{0} + 4 \cdot \frac{1}{8} \cdot v_{0} + 4^{2} \cdot \frac{1}{8^{2}} v_{0} + 4^{3} \cdot \frac{1}{8^{3}} v_{0} + 4^{4} \cdot \frac{1}{8^{4}} v_{0} + . . .$

$v = v_{0} + \frac{1}{2} v_{0} + \frac{1}{2^{2}} v_{0} + \frac{1}{2^{3}} v_{0} + . . . = \frac{v_{0}}{1 - \frac{1}{2}} = 2 v_{0}$

$v = 2 \cdot \frac{π \sqrt{6}}{216} a^{3} = \frac{π \sqrt{6}}{108} a^{3}$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!