Dissertativas 6 - ITA - 2ª Fase Dia 3 - ITA 2025

Selecione uma prova

Gabarito

Física
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS
11. TXTTXT

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 6

Dissertativa

Uma sonda tripulada foi projetada para resistir ao calor da atmosfera de mercúrio, que pode atingir uma temperatura $T_{0} = 430 ° C$ . A sonda tem uma estrutura semelhante à de uma casca esférica composta por duas camadas, como mostra a figura. A camada externa, de espessura $d_{1}$ , é composta por um material rígido de condutividade térmica $K_{1}$ . A camada interna, de espessura $d_{2}$ , é composta por um material termorresistente e isolante térmico de condutividade térmica $K_{2}$ . O raio externo da estrutura é igual a R.

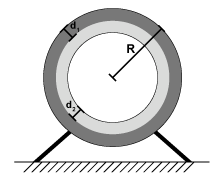
Considerando a situação descrita acima, faça o que se pede nos itens a seguir.

a) Expresse a condutividade térmica efetiva da sonda em função de $R, K_{1}, K_{2} e d,$ em que $d = d_{1} = d_{2} e R ≫ d .$

b) Estime a potência, em kW, que um refrigerador deve ter para manter a temperatura interna da sonda em $T_{i} = 23 ° C$ , assumindo que $R$ = 20 m, $d_{1} = d_{2}$ = 30 cm, $K_{1}$ = 50 W/( $m °$ C), $K_{2}$ = 0, 020 W/( $m °$ C) e que a máquina refrigeradora tem um coeficiente de performance ideal.

Resolução:

a) Pela equação de Fourier para condutor esférico:

$ϕ = K \cdot A \frac{d T}{d r} \Rightarrow ϕ = K \cdot 4 {πr}^{2} \cdot \frac{d T}{d r} \int_{T_{1}}^{T_{2}} d T = \frac{ϕ}{4 πK} \cdot \int_{r_{1}}^{r_{2}} r^{- 2} d r T_{2} - T_{1} = \frac{ϕ}{4 πK} \cdot (\frac{1}{r_{1}} - \frac{1}{r_{2}}) ∆ T = \frac{1}{4 πK} \cdot (\frac{r_{2} - r_{1}}{r_{1} \cdot r_{2}}) \cdot ϕ$

Pelo análogo elétrico, a resistência térmica vale: $R_{t} = \frac{1}{4 πK} \cdot (\frac{r_{2} - r_{1}}{r_{1} \cdot r_{2}})$

Como $d_{1} = d_{2} = d$ , temos:

$R_{1} = \frac{1}{4 {πK}_{1}} \cdot \frac{d}{R (R - d)}, R_{2} = \frac{1}{4 {πK}_{2}} \cdot \frac{d}{(R - d) (R - 2 d)} e R_{eq} = \frac{1}{4 {πK}_{eq}} \cdot \frac{2 d}{R (R - 2 d)}$

Como temos uma associação em série:

$R_{eq} = R_{1} + R_{2} \frac{1}{4 {πK}_{eq}} \cdot \frac{2 d}{R (R - 2 d)} = \frac{1}{4 {πK}_{1}} \cdot \frac{d}{R (R - d)} + \frac{1}{4 {πK}_{2}} \cdot \frac{d}{(R - d) (R - 2 d)} \frac{1}{K_{eq}} \cdot \frac{2}{R (R - 2 d)} = \frac{1}{K_{1}} \cdot \frac{1}{R (R - d)} + \frac{1}{K_{2}} \cdot \frac{1}{(R - d) (R - 2 d)} \frac{2}{K_{eq}} = \frac{1}{K_{1}} \cdot \frac{R (R - 2 d)}{R (R - d)} + \frac{1}{K_{2}} \cdot \frac{R (R - 2 d)}{(R - d) (R - 2 d)} \frac{2}{K_{eq}} = \frac{1}{K_{1}} \cdot \frac{(R - 2 d)}{(R - d)} + \frac{1}{K_{2}} \cdot \frac{R}{(R - d)} \frac{2}{K_{eq}} = \frac{1}{(R - d)} \cdot \frac{(R - 2 d) \cdot K_{2} + R \cdot K_{1}}{K_{1} \cdot K_{2}} K_{eq} = \frac{2 \cdot (R - d) \cdot K_{1} \cdot K_{2}}{(R - 2 d) \cdot K_{2} + R \cdot K_{1}}$

Considerando R >> d: $K_{eq} = \frac{2 K_{1} \cdot K_{2}}{K_{1} + K_{2}}$

Observação: como R >> d, poderíamos fazer uma solução mais simples sem o cálculo integral e que levaria ao mesmo resultado:

Pela equação de Fourier:

$ϕ = \frac{K \cdot A \cdot ∆ T}{d} \Rightarrow ∆ T = \frac{d}{K \cdot A} \cdot ϕ$

Pelo análogo elétrico, a resistência térmica vale: $R_{t} = \frac{d}{K \cdot A}$

Logo: $R_{1} = \frac{d_{1}}{K_{1} \cdot A_{1}} e R_{2} = \frac{d_{2}}{K_{2} \cdot A_{2}}$

Como temos uma associação em série:

$R_{eq} = R_{1} + R_{2} = \frac{d_{1}}{K_{1} \cdot A_{1}} + \frac{d_{2}}{K_{2} \cdot A_{2}}$

Como $d_{1} = d_{2} = d e R ≫ d$ , temos: $A_{1} = A_{2} = 4 {πR}^{2}$

Logo: $R_{eq} = \frac{d}{4 {πR}^{2}} \cdot \frac{K_{1} + K_{2}}{K_{1} \cdot K_{2}} (i)$

Mas a resistência térmica equivalente é dada por: $R_{eq} = \frac{2 d}{K_{eq} \cdot 4 {πR}^{2}} (ii)$

De (i) e (ii):

$\frac{d}{4 {πR}^{2}} \cdot \frac{K_{1} + K_{2}}{K_{1} \cdot K_{2}} = \frac{2 d}{K_{eq} \cdot 4 {πR}^{2}} \Rightarrow K_{eq} = \frac{2 K_{1} \cdot K_{2}}{K_{1} + K_{2}}$

b) Condutividade térmica efetiva:

$K_{eq} = \frac{2 K_{1} \cdot K_{2}}{K_{1} + K_{2}} = \frac{2 \cdot 50 \cdot 0, 02}{50 + 0, 02} = \frac{2}{50, 02} \frac{W}{m} \cdot ° C$

Fluxo de calor que entra:

$ϕ = 4 {πK}_{eq} (\frac{r_{int} r_{ext}}{r_{ext} - r_{int}}) \cdot ∆ T = 4 {πK}_{eq} \cdot [\frac{R \cdot (R - 2 d)}{2 d}] \cdot ∆ T$

Considerando R >>d:

$ϕ = \frac{K_{eq} \cdot 4 {πR}^{2} \cdot ∆ T}{2 d} = \frac{2}{50, 02} \cdot \frac{4 π \cdot 20^{2} \cdot 407}{2 \cdot 0, 3}$

$ϕ = 136, 3 kW$

Para se manter a temperatura interna constante, a taxa de retirada de calor do refrigerador deve ser:

$Q_{f} = ϕ = 136, 3 kW$

Para refrigerador de Carnot (coeficiente de performance ideal):

$β = \frac{Q_{f}}{P_{refri}} = \frac{T_{f}}{T_{q} - T_{f}} \Rightarrow \frac{136, 3}{P_{refri}} = \frac{296}{407} \Rightarrow P_{refri} = 187, 4 kW$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!