Questão 178 - Dia 2 - Cinza - Enem 2025

Novidade! Correção inteligente - simulado seus resultados.

Assista agora ao Poliedro Resolve do 1º dia do Enem 2025

Selecione uma prova

Gabarito

Geral
1. 91C
2. 92D
3. 93A
4. 94E
5. 95A
6. 96A
7. 97C
8. 98B
9. 99D
10. 100D
11. 101E
12. 102C
13. 103E
14. 104E
15. 105B
16. 106D
17. 107E
18. 108A
19. 109B
20. 110B
21. 111C
22. 112B
23. 113B
24. 114D
25. 115E
26. 116E
27. 117E
28. 118C
29. 119B
30. 120B
31. 121D
32. 122C
33. 123D
34. 124C
35. 125B
36. 126A
37. 127A
38. 128B
39. 129D
40. 130D
41. 131C
42. 132D
43. 133C
44. 134E
45. 135A
46. 136A
47. 137D
48. 138D
49. 139B
50. 140B
51. 141C
52. 142E
53. 143C
54. 144E
55. 145C
56. 146C
57. 147B
58. 148D
59. 149D
60. 150D
61. 151E
62. 152C
63. 153A
64. 154C
65. 155E
66. 156A
67. 157B
68. 158D
69. 159E
70. 160B
71. 161E
72. 162C
73. 163C
74. 164D
75. 165B
76. 166A
77. 167B
78. 168E
79. 169AD
80. 170A
81. 171A
82. 172B
83. 173C
84. 174C
85. 175B
86. 176E
87. 177A
88. 178D
89. 179D
90. 180E

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 178

Objetiva

178

Quatro amigos, cada um com 100 moedas, criaram um jogo, no qual cada um assume uma das quatro posições 1, 2, 3 ou 4, indicadas na figura, e nela permanece até o final.

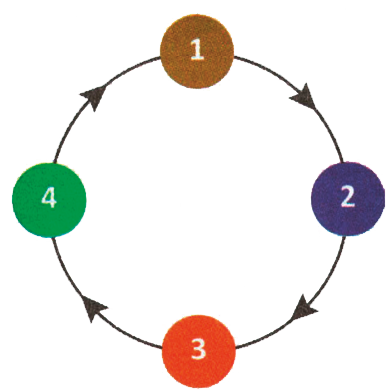
O desenvolvimento do jogo se dá em rodadas e, em todas elas, cada jogador transfere e recebe uma quantidade de moedas da seguinte maneira:

o jogador na posição 1 transfere 1 moeda para o jogador na posição 2;
o jogador na posição 2 transfere 2 moedas para o jogador na posição 3;
o jogador na posição 3 transfere 3 moedas para o jogador na posição 4;
o jogador na posição 4 transfere 4 moedas para o jogador na posição 1, completando a rodada.

Ao final da rodada n, qual é a expressão algébrica que representa o número de moedas do jogador na posição 1?

Alternativas

A
$103 + 4 n$
B
$103 + 3 n$
C
$100 + 4 n$
D
$100 + 3 n$
E
$99 + 4 n$

Gabarito:
D

Rodada 1:

Jogador 1: 100 moedas

Jogador 1 transfere 1 moeda e recebe 4 moedas $\Rightarrow$ Ficando com 103 moedas

Rodada 2:

Jogador 1: 103 moedas

Jogador 1 transfere 1 moeda e recebe 4 moedas $\Rightarrow$ Ficando com 106 moedas

Rodada 3:

Jogador 1: 106 moedas

Jogador 1 transfere 1 moeda e recebe 4 moedas $\Rightarrow$ Ficando com 109 moedas

Logo:

Rodada 1) 100 + 3

Rodada 2) 100 + 2 $\cdot$ 3

Rodada 3) 100 + 3 $\cdot$ 3

Rodada n) $100 + 3 n$

178

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!