Dissertativas 4 - 2ª Fase Dia 3 - ITA 2025

Poliedro Resolve Resolução - ITA 2ª Fase Dia 4 - 2025

Resolução - Poliedro Resolve - ITA 2025 Dia 3 - 2025

Resolução - Poliedro Resolve - ITA 2ª Fase Dia 2 - 2025

Poliedro Resolve Resolução - ITA 2ª Fase Dia 1 - 2025

Selecione uma prova

Gabarito

Física
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS
11. TXTTXT

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 4

Dissertativa

Um objeto de massa m se movimenta em direção a outro objeto de massa M inicialmente em repouso. Após a colisão, a velocidade dos objetos forma, respectivamente, ângulos $α$ e $θ$ com a horizontal. Faça o que se pede nos itens a seguir.

a) Determine as expressões para os módulos de ${\vec{v}}_{1}$ e ${\vec{v}}_{2}$ em função de $α$ , $θ$ e v.
b) Denotando a variação relativa entre a energia cinética final e inicial do sistema por $δ$ , determine a razão m/M em função de $θ$ e $δ$ , para $α$ = 90°.
c) Calcule o valor numérico da razão M/m, para $θ$ = 30°, $α$ = 90° e perda relativa de 60% de energia cinética depois da colisão.

Resolução:

$sen (θ + 90 °) = senθ \cdot \cos 90 ° + sen 90 ° \cdot cosθ$

$a) p_{x} = cte : m \cdot v = m \cdot v_{2} \cdot cosα + M \cdot v_{1} \cdot cosθ p_{y} = cte : 0 = m \cdot v_{2} \cdot senα - M \cdot v_{1} \cdot senθ m \cdot v \cdot senθ = m \cdot v_{2} \cdot cosα \cdot senθ + M \cdot v_{1} \cdot cosθ \cdot senθ \frac{0 = m \cdot v_{2} \cdot senα \cdot cosθ - M \cdot v_{1} \cdot senθ \cdot cosθ}{m \cdot v \cdot senθ = m \cdot v_{2} (senθ \cdot cosα + senα \cdot cosθ)} v \cdot senθ = v_{2} \cdot sen (θ + α) \Rightarrow v_{2} = \frac{v \cdot senθ}{sen (θ + α)}$

$\frac{m \cdot v \cdot senα = m \cdot v_{2} \cdot cosα \cdot senα + M \cdot v_{1} \cdot cosθ \cdot senα 0 = m \cdot v_{2} \cdot senα \cdot cosα - M \cdot v_{1} \cdot senθ \cdot cosα}{m \cdot v \cdot senα = M \cdot v_{1} \cdot (cosθ \cdot senα + senθ \cdot cosα)}$

$v_{1} = \frac{m \cdot v \cdot senα}{M \cdot sen (θ + α)}$

$b) δ = \frac{E_{M, F} - E_{M, I}}{E_{M, I}} = \frac{E_{M, F}}{E_{M, I}} - 1 δ = \frac{\frac{1}{2} m \cdot v_{2}^{2} + \frac{1}{2} M \cdot v_{1}^{2}}{\frac{1}{2} m \cdot v^{2}} - 1 δ = \frac{m \cdot v_{2}^{2} + M \cdot v_{1}^{2}}{m \cdot v^{2}} - 1 = \frac{\frac{m \cdot v^{2} \cdot {sen}^{2} θ}{{sen}^{2} (θ + α)} + \frac{M \cdot m^{2} \cdot v^{2} \cdot {sen}^{2} α}{M^{2} \cdot {sen}^{2} (θ + α)}}{m \cdot v^{2}} - 1 δ = \frac{{sen}^{2} θ}{{sen}^{2} (θ + α)} + \frac{m}{M} \cdot \frac{{sen}^{2} α}{{sen}^{2} (θ + α)} - 1 δ + 1 = \frac{{sen}^{2} θ}{{sen}^{2} (θ + 90)} + \frac{m}{M} \cdot \frac{{sen}^{2} 90}{{sen}^{2} (θ + 90)} (δ + 1) \cdot \cos^{2} θ = {sen}^{2} θ + \frac{m}{M} \cdot 1 \Rightarrow \frac{m}{M} = (δ + 1) \cos^{2} θ - {sen}^{2} θ$

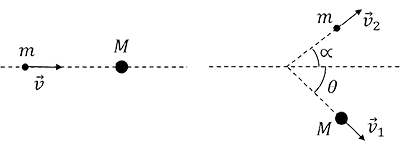
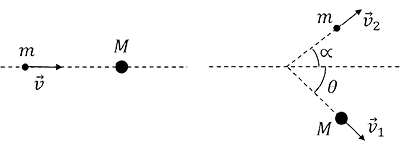
c) Perda de 60%:

$\frac{E_{M, I} - E_{M, F}}{E_{M, I}} = 60 % = 0, 6 \Rightarrow δ = - 0, 6 Se θ = 30 ° : \frac{m}{M} = (- 0, 6 + 1) \cos^{2} 30 ° - {sen}^{2} 30 ° \frac{m}{M} = 0, 4 \cdot \frac{3}{4} - \frac{1}{4} = \frac{1, 2 - 1}{4} = \frac{0, 2}{4} \frac{M}{m} = \frac{4}{0, 2} \Rightarrow \frac{M}{m} = 20$

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!