Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

Considere um objeto de massa que se movimenta sobre uma cunha de massa , inclinação e coeficiente de atrito . A cunha se move horizontalmente para a direita, sob a ação de uma força em uma superfície lisa. Considere que, inicialmente, o sistema se encontra em repouso, com esse objeto no topo da cunha. Sabe-se que o intervalo de tempo que ele leva para chegar ao solo com a cunha em movimento é o triplo do que levaria se a cunha estivesse fixa. Com base nessas informações, calcule, em função de , a magnitude
__080f2e4b-bdb0-49e1-a071-b76016e97143.png)
a) da aceleração da cunha;
b) da força normal que o plano inclinado faz no objeto;
c) da força .
a) No caso da cunha fixa, tem-se:
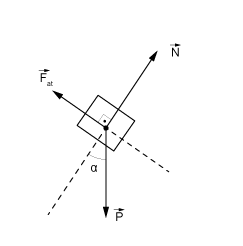
Utilizando a equação horária do MUV, tem-se:
No caso da cunha em movimento, considerando o referencial acelerado da cunha, tem-se:
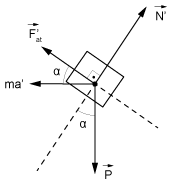
Analogamente:
Mas, , assim:
b) Da equação do eixo normal no caso da cunha em movimento, tem-se:
c)
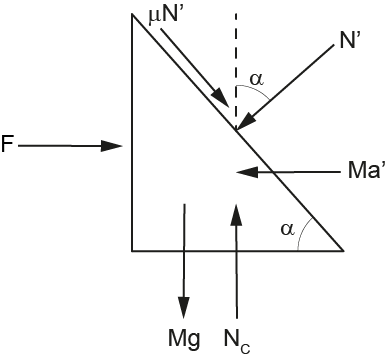
Do equilíbrio horizontal da cunha no referencial não inercial:
Substituindo os resultados anteriores, tem-se:
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!