Questão 73 - Conhecimentos Gerais - Santa Casa 2025

Para resolver este exercício, podemos supor que o total de alunos que concluíram o Ensino Médio foi 100.

Como 20% deles foram aprovados em algum vestibular, o número de aprovados foi 20.

Da mesma forma, como 40% deles tinham feito cursinho, a quantidade de alunos que fizeram cursinho foi 40.

Por fim, o enunciado informa que a probabilidade de um aluno que fez cursinho ter sido aprovado no vestibular é de $\frac{3}{8}$. Como 40 alunos fizeram cursinho, então o número n de estudantes que fizeram cursinho e foram aprovados é:

$\mathrm{n} = \frac{3}{8} · 40 = 15$

Representando essa situação por meio de um diagrama de Venn-Euler, tem-se:

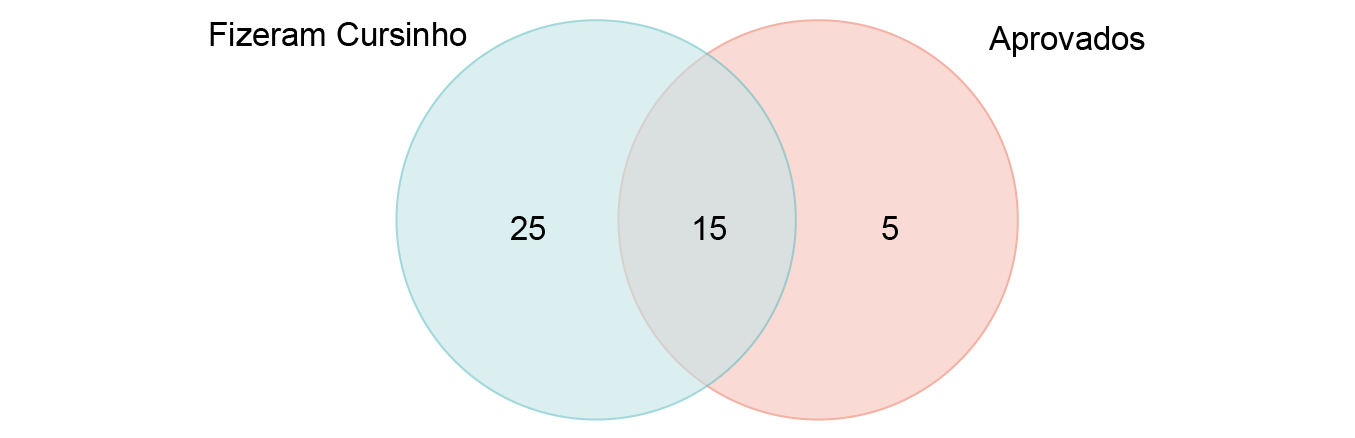
O enunciado pede a probabilidade P de que um estudante aprovado no vestibular tenha feito cursinho. Como se sabe que o estudante foi aprovado, o espaço amostral será apenas o conjunto dos aprovados, ou seja, $\mathrm{n}\left(\mathrm{\Omega }\right) = 20$. Por fim, os casos favoráveis são os indivíduos que fizeram cursinho E foram aprovados, ou seja, a interseção dos dois conjuntos. Logo, n(E) = 15 e:

$\mathrm{P}=\frac{15}{20} = \frac{3}{4}$

Resolução alternativa:

Interpretando a probabilidade pedida com uma probabilidade condicional, tem-se:

$\mathrm{P}\left(\mathrm{C}|\mathrm{A}\right) = \frac{\mathrm{n}\left(\mathrm{C}\cap \mathrm{A}\right)}{\mathrm{n}\left(\mathrm{A}\right)} = \frac{{\displaystyle \frac{3}{8} }· 40}{20} = \frac{15}{20} = \boxed{\frac{3}{4}}$