Dissertativas 7 - 2ª Fase Dia 2 - IME 2025

Poliedro Resolve - Resolução IME 1ª Fase 2025

Poliedro Resolve Resolução - IME 2ª Fase Dia 1 - 2025

Poliedro Resolve Resolução - IME 2ª Fase Dia 2 - 2025

Selecione uma prova

Gabarito

Física
1. 1DIS
2. 2DIS
3. 3DIS
4. 4DIS
5. 5DIS
6. 6DIS
7. 7DIS
8. 8DIS
9. 9DIS
10. 10DIS

Questão ativa
Já visualizadas
Não visualizadas
Resolução pendente
ANL
Questão anulada
S/A
Sem alternativas

Questão 7

Dissertativa

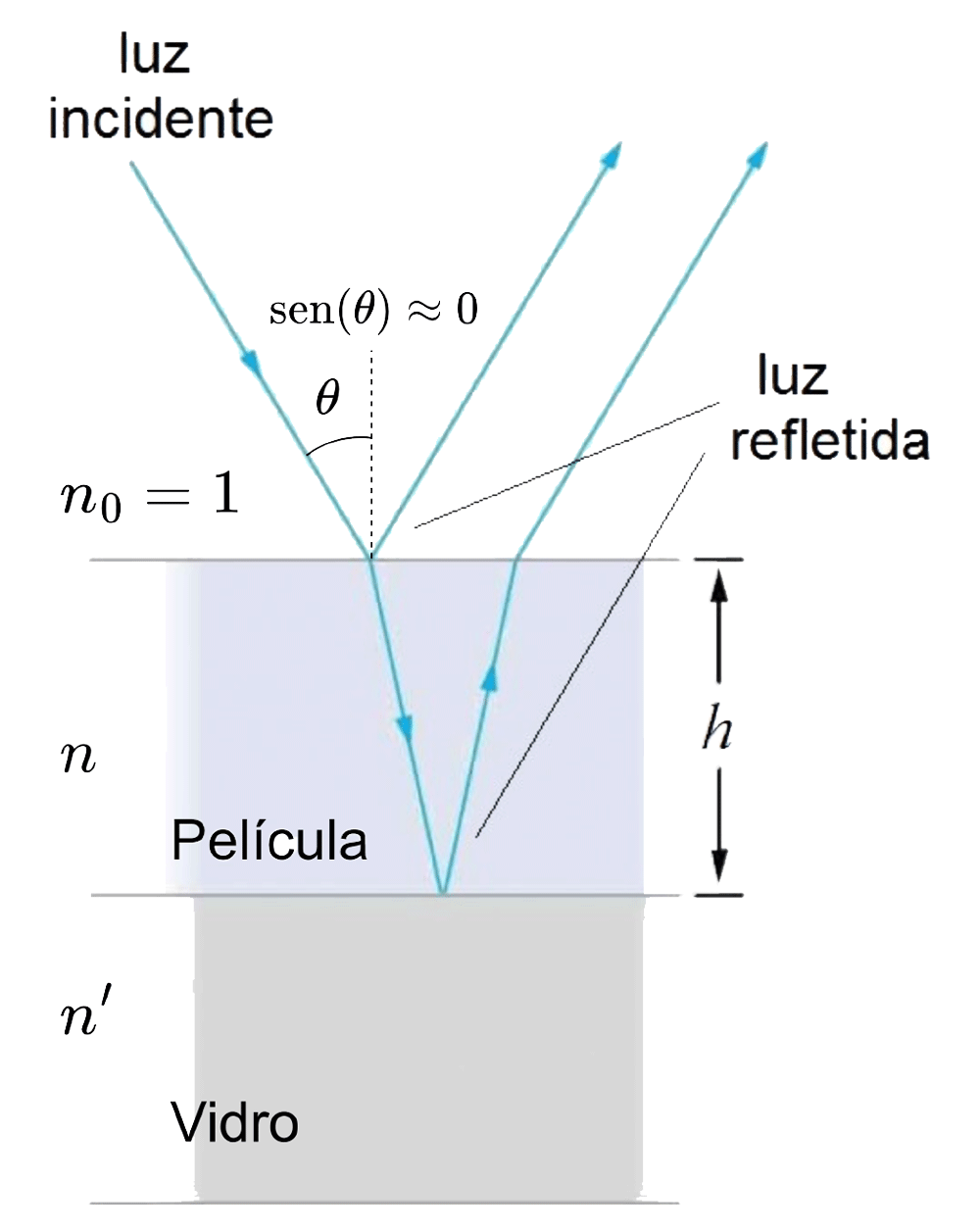
Uma onda de luz plana e monocromática propaga-se no vácuo e incide quase perpendicularmente sobre uma película depositada sobre uma placa de vidro. As ondas refletidas pela película e pelo vidro sofrem interferência completamente destrutiva ao retornarem ao vácuo para três valores de comprimento de onda da luz incidente, sendo dois deles conhecidos.

Dados:

1º comprimento de onda no vácuo conhecido para a ocorrência de interferência destrutiva: $λ_{1}$ ;
2º comprimento de onda no vácuo conhecido para a ocorrência de interferência destrutiva: $λ_{2}$ ;
$λ_{1} > λ_{2}$ ;
índice de refração da película: $n$ ;
índice de refração do vidro: $n'$ ;
$n' > n$ .

Observações:

o ângulo de incidência pode não corresponder ao da figura meramente ilustrativa;
o valor do 3º comprimento de onda no vácuo para a ocorrência de interferência destrutiva está entre $λ_{1}$ e $λ_{2}$ .

Determine:

a) a espessura $h$ da película, indicada na figura, em função dos dados acima listados;
b) o valor do terceiro comprimento de onda para interferência destrutiva;
c) os valores de comprimento de onda no vácuo para o caso de haver interferência construtiva.

Resolução:

Resolução:

Para incidência praticamente normal, a diferença de caminho óptico é dada por:

$Δd = 2 nh$

Como $n > 1$ e $n' > n$ , ocorre inversão de fase em ambas as reflexões. Assim, para interferência destrutiva:

$Δd = n_{i} \cdot \frac{λ}{2}$ , em que $n_{i}$ é um número ímpar.

$\Rightarrow 2 nh = n_{i} \cdot \frac{λ}{2} \Rightarrow λ = \frac{4 nh}{n_{1}}$

Assim: $λ_{1} = \frac{4 nh}{n_{i}}, λ_{3} = \frac{4 nh}{n_{i} + 2}, λ_{2} = \frac{4 nh}{n_{i} + 4}$

$n_{i} + 4 = \frac{4 nh}{λ_{2}}, n_{i} = \frac{4 nh}{λ_{1}} \Rightarrow 4 = 4 nh (\frac{1}{λ_{2}} - \frac{1}{λ_{1}}) \Rightarrow 1 = nh \frac{(λ_{1} - λ_{2})}{λ_{1} λ_{2}} \Rightarrow h = \frac{λ_{1} λ_{2}}{n (λ_{1} - λ_{2})}$

$n_{i} + 2 = \frac{4 nh}{λ_{3}} \Rightarrow \frac{4 nh}{λ_{1}} + 2 = \frac{4 nh}{λ_{3}} \Rightarrow 2 = 4 nh (\frac{1}{λ_{3}} - \frac{1}{λ_{1}}) \Rightarrow 1 = 2 \cdot \frac{(λ_{1} λ_{2})}{λ_{1} - λ_{2}} \cdot \frac{(λ_{1} - λ_{3})}{λ_{1} λ_{3}} \Rightarrow λ_{3} (λ_{1} - λ_{2}) = 2 λ_{2} (λ_{1} - λ_{3}) \Rightarrow λ_{1} λ_{3} - λ_{2} λ_{3} = 2 λ_{1} λ_{2} - 2 λ_{2} λ_{3} \Rightarrow λ_{3} (λ_{1} + λ_{2}) = 2 λ_{1} λ_{2} \Rightarrow λ_{3} = \frac{2 λ_{1} λ_{2}}{λ_{1} + λ_{2}}$

c) Para interferência construtiva: $Δd = k \cdot λ, k \in ℤ^{*}$

$\Rightarrow 2 nh = k \cdot λ \Rightarrow 2 \cdot \frac{λ_{1} λ_{2}}{λ_{1} - λ_{2}} = k \cdot λ \Rightarrow λ = \frac{2 λ_{1} λ_{2}}{λ_{1} - λ_{2}} \cdot \frac{1}{k}, k \in ℤ^{*}$

Observação: para que ocorra interferência destrutiva, cada comprimento de onda deve estar associado a um número ímpar. No entanto, apesar de o enunciado dizer que $λ_{1} > λ_{3} > λ_{2}$ , não fica claro se esses comprimentos de onda estão associados a números ímpares consecutivos. Toda a resolução apresentada foi construída levando isso em conta, porém, caso essa consideração não fosse feita, não haveria como relacionar os comprimentos de onda, o que impossibilitaria a resolução da questão.

Downloads

Provas

Fique por dentro das novidades

Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!