Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

No estudo de ondas que se propagam em meios elásticos, a impedância característica de um material é dada pelo produto da sua densidade pela velocidade da onda nesse material, ou seja, z = µv. Sabe-se, também, que uma onda de amplitude , que se propaga em um meio 1 ao penetrar em uma outra região, de meio 2, origina ondas, refletida e transmitida, cuja amplitudes são, respectivamente:
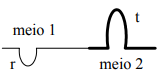
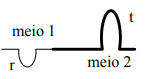
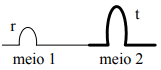
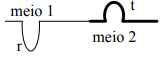
Num fio, sob tensão τ, a velocidade da onda nesse meio é dada por . Considere agora o caso de uma onda que se propaga num fio de densidade linear µ (meio 1) e penetra num trecho desse fio em que a densidade linear muda para 4µ (meio 2). Indique a figura que representa corretamente as ondas refletidas (r) e transmitida (t).
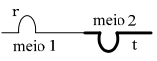


Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!