Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

Prove que o volume de um prisma triangular é igual ao semiproduto da área de uma face lateral pela distância desta face à sua aresta oposta.
Na figura a seguir, ABCDEF é o prisma triangular com aresta lateral de comprimento L. A secção reta do prisma é o triângulo PQR de lados com medidas a, b e c.
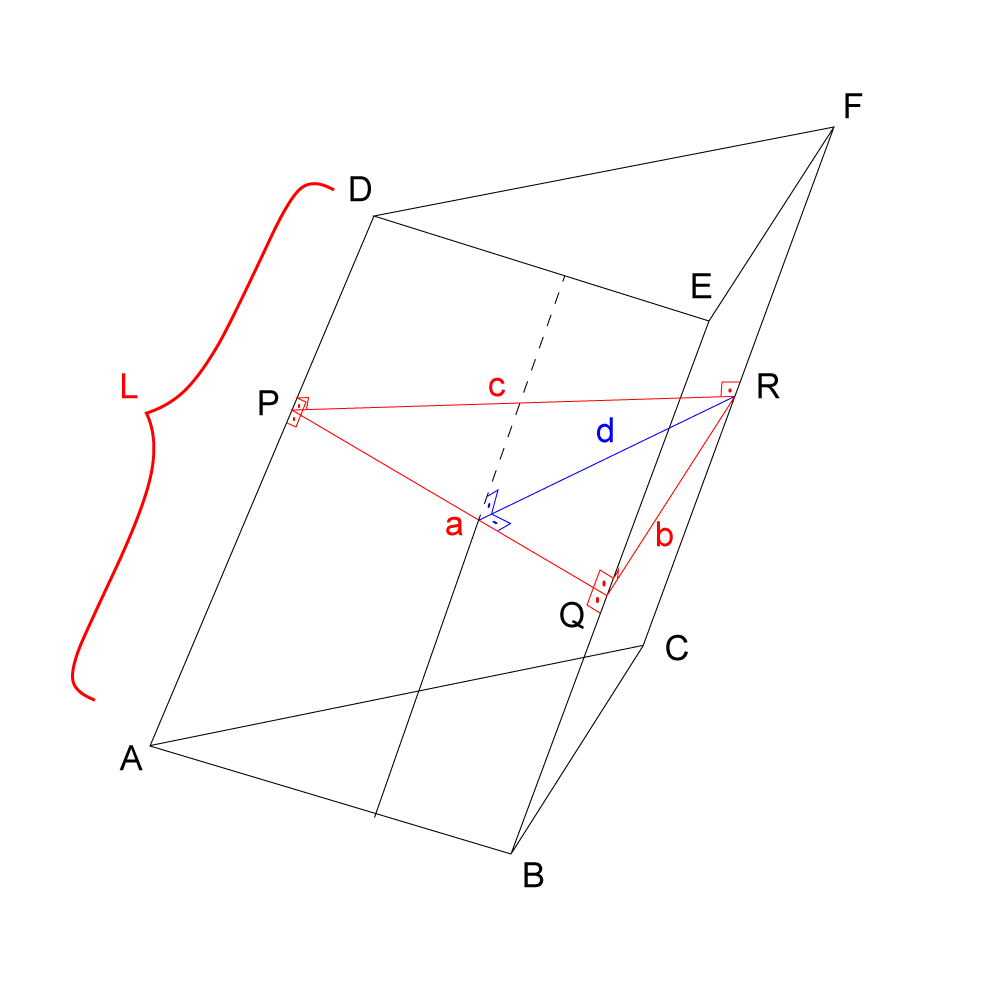
Sabe-se que:
Assim, da figura:
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!