Fique por dentro das novidades
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!

A circunferência C tem equação . Seja C' uma circunferência de raio 1 que se desloca tangenciando internamente a circunferência C, sem escorregamento entre os pontos de contato, ou seja, C' rola internamente sobre C.
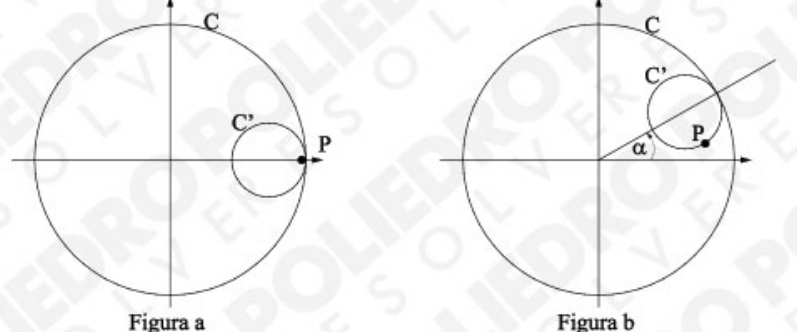
Define-se o ponto P sobre C' de forma que no início do movimento de C' o ponto P coincide com o ponto de tangência (4,0), conforme figura a. Após certo deslocamento, o ângulo de entre o eixo x e a reta que une o centro das circunferências é , conforme figura b.
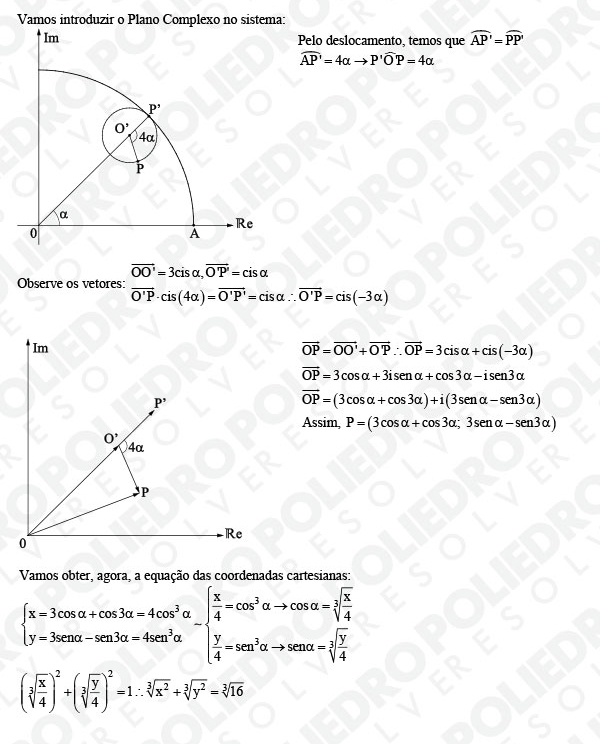
IME 2016 - 2ª Fase
Inscreva-se em nossa newsletter para receber atualizações sobre novas resoluções, dicas de estudo e informações que vão fazer a diferença na sua preparação!