Dissertativa 7 - Matemática - IME 2004

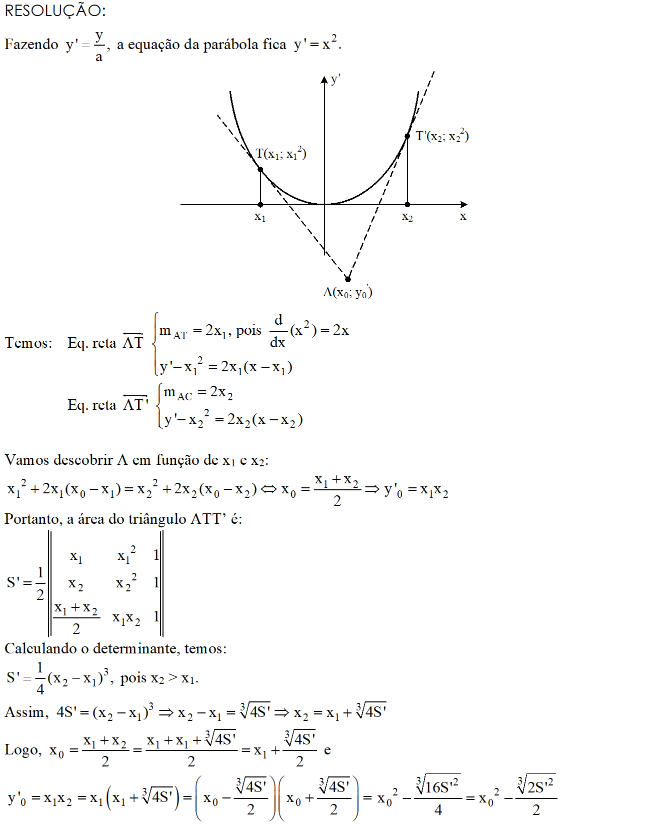
Considere a parábola P de equação y = a${\mathrm{x}}^2$, com a > 0 e um ponto A de coordenadas (${\mathrm{x}}_0$, ${\mathrm{y}}_0$) satisfazendo a ${\mathrm{y}}_0$ < $a{x_0}^2$. Seja S a área do triângulo ATT’, onde T e T’ são os pontos de contato das tangentes a P passando por A.

a) Calcule o valor da área S em função de a, ${\mathrm{x}}_0$ e ${\mathrm{y}}_0$.

b) Calcule a equação do lugar geométrico do ponto A, admitindo que a área S seja constante.

c) Identifique a cônica representada pela equação obtida no item anterior.